Eine Vierfeldertafel ist eine Darstellungsweise für zwei Ereignisse, die gemeinsam betrachtet werden. Mit dem Baumdiagramm kann man bedingte Wahrscheinlichkeiten darstellen.
Was ist eine Vierfeldertafel?
Mit einer Vierfeldertafel kannst du zwei Ereignisse darstellen und miteinander in Bezug setzen. Du kannst relative und absolute Häufigkeiten angeben.
Die Logik ist wie folgt:
| Merkmal 1 | Merkmal 2 | gesamt | |
| Stichprobe 1 | a | b | a + b |
| Stichprobe 2 | c | d | c + d |
| gesamt | a + c | b + d | n = a + b + c + d |
Im Beispiel werden 200 Schülerinnen und Schüler befragt, ob sie Mathe lieben oder hassen. In den Spalten finden sich Schüler und Schülerinnen und in den Zeilen Mathe-Liebe oder Mathe-Hass. Die Gesamtzahlen ergeben addiert dann den Spaltenwert oder Zeilenwert und die Summe der Gesamtzellen ergibt 200.

Umrechnung einer Vierfeldertafel in ein Baumdiagramm
Wenn du eine Vierfeldertafel in ein Baumdiagramm umrechnen möchtest, musst du eventuell aus den absoluten Werten eine relative Häufigkeit machen.
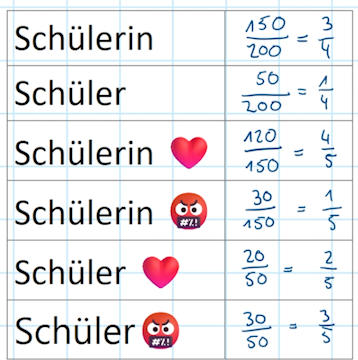
Im Beispiel habe ich P(Schüler) und P(Schülerin) genommen, was die Gesamtzahl der Schülerinnen bzw. die Gesamtzahl der Schüler geteilt durch die Gesamtzahl an Personen ist. Davon abhängig sind dann die Werte Mathe-Liebe und Mathe-Hass.

In Worten sagt die Formel: „Die Wahrscheinlichkeit von A unter der Bedingung B ist gleich der Wahrscheinlichkeit von A geschnitten mit der Wahrscheinlichkeit von B geteilt durch die Wahrscheinlichkeit von B.“
In anderen Worten ist die Wahrscheinlichkeit, eine Mathe liebende Schülerin zu wählen, dass eine Person Mathe liebt unter der Voraussetzung, dass es eine Schülerin ist gleich der Schnittmenge von Mathe lieben und Schülerin geteilt durch die Gesamtzahl der Schülerinnen. Es entsteht auch hier ein Bruch, der aber in Abhängigkeit von dem ersten Ereignis steht. Man spricht hier von einer bedingten Wahrscheinlichkeit. Es ist auch ein Unterschied, ob die beiden Ereignisse stochastisch unabhängig sind.

Das Ganze ist in dieser Tabelle abzulesen. Wie du siehst, hat Stufe 1 als Nenner Viertel. Bei der zweiten Stufe ergeben sich Fünftel. Bei anderen Zahlen hätten sich natürlich auch unterschiedliche Nenner auf der zweiten Stufe ergeben können.
Der nächste Schritt ist einfach, denn nun musst du nur noch die Brüche ins Baumdiagramm eintragen.




Schreib mir einen Kommentar!