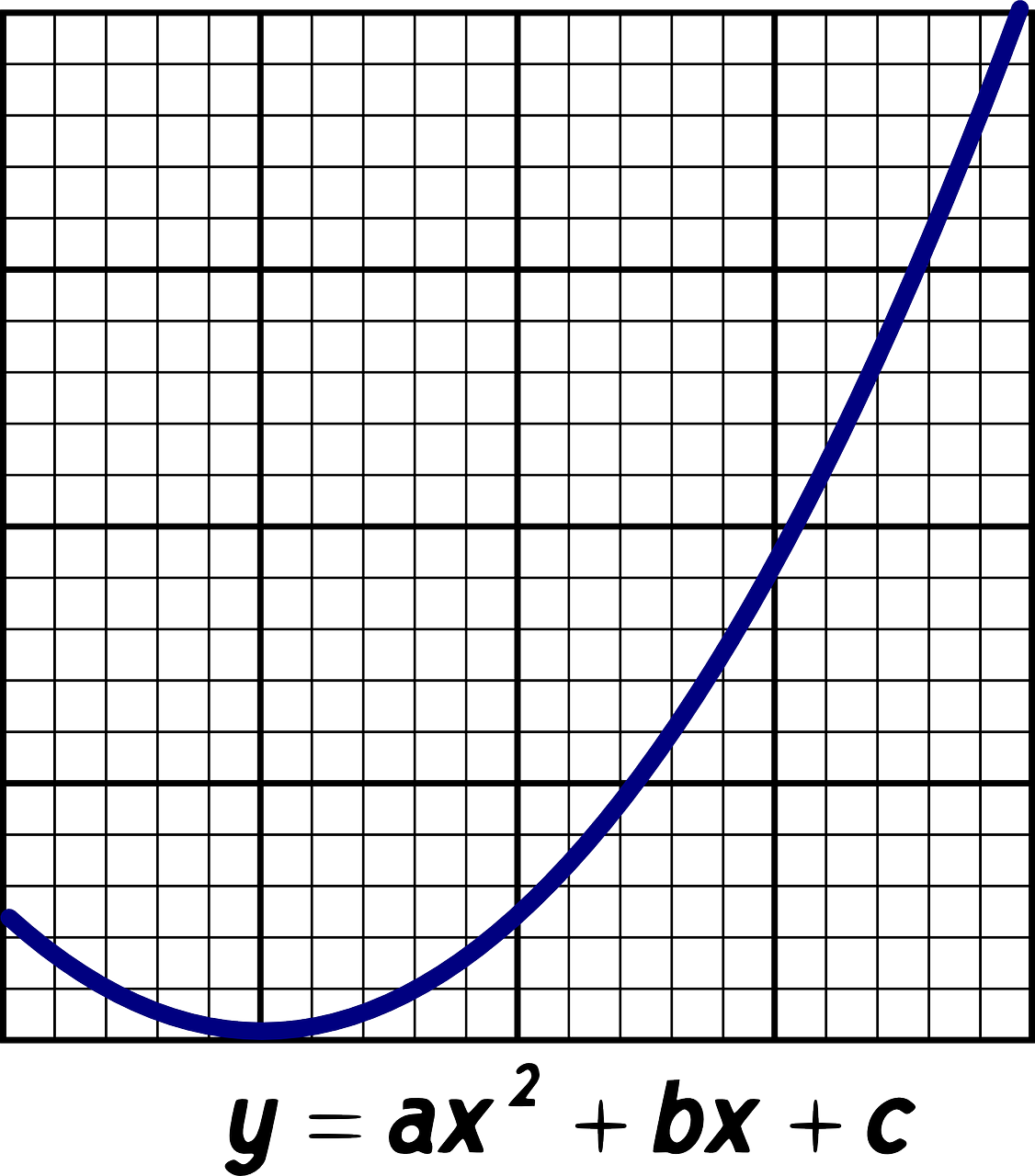
Viele Menschen wissen mit quadratischen Funktionen und Parabeln überhaupt nichts anzufangen. Dabei sind Parabeln überall um uns herum und ein gewisses Verständnis haben wir alle und trotzdem bringen kaum andere mathematische Themen so viel Frust und Fragen mit sich wie die quadratischen Funktionen.
Wenn zum Beispiel jemand einen Fußball schießt, steigt er zunächst immer steiler in die Höhe. Je höher er fliegt, umso weniger stark steigt er. An einem Punkt beginnt er wieder zu fallen. Diesen Punkt nennt man Scheitelpunkt. Anschließend fällt der Ball langsam und immer schneller in Richtung Boden. Geschickte Fußballer schaffen es, den Ball so zu kicken, dass er mal steiler und mal flacher fliegt und können dadurch sogar Gegenspieler überspielen.
Auch bei Brücken finden wir oft Parabeln, welche die Bögen unterhalb der Brücke zur Stabilisierung nutzen. Auch in alten Gewölben finden sich oft Parabeln wieder, weil diese statisch wünschenswerte Eigenschaften mit sich bringen.

(Bild: Pixabay/ Openclipart-Vectors)
In meiner Playlist von Lernsnacks zum Thema Parabeln habe ich einige Videos zusammengestellt, in denen ich alle wichtigen Punkte zu Parabeln erkläre und auch probiere, ihre Bedeutung für unsere Umwelt und unser Leben zu beschreiben.
Im Wesentlichen lassen sich Parabeln an einigen Merkmalen unterscheiden.
- Der Scheitelpunkt ist der Punkt, an dem die Parabel ihre Richtung ändert.
- Die Parabel kann an der Y-Achse verschoben werden.
- Die Öffnung der Parabel wird durch das Vorzeichen bestimmt: f(x) = x² öffnet sich nach oben und f(x) = -x² öffnet sich nach unten.
- Gestauchte Parabeln steigen erheblich langsamer an als gestreckte Parabeln.
- Nicht zuletzt gibt es noch die Scheitelform und die Normalform
Schwierig ist die korrekte Anwendung der Formeln.
- Die Formel f(x) = x² und f(x) = -x² beschreiben nach oben oder unten geöffnete Normalparabeln.
- Die Formel f(x) = +/- ax² +/- c zeigt im Wert a an, ob die Parabel gestreckt oder gestaucht ist und der Wert c steht für die Verschiebung an der Y-Achse
- Die Scheitelpunktform f(x) = +/- a(x+/-d)² +/- e ermöglicht es, den Scheitelpunkt sofort abzulesen. Dabei muss das Vorzeichen von d vertauscht werden und e wird übernommen.
- Die Nullstellen einer Parabel lassen sich mit f(x) = +/- ax² +/- px +/- q und der PQ-Formel berechnen.
Die wichtigsten Unterscheidungen von Parabeln erkläre ich im folgenden Lernsnack:
Lesen Sie im nächsten Artikel über Flächeninhalte zusammengesetzter Figuren.